A Quoi Sert La Réciproque Du Théorème De Thalès

À quoi sert le théorème de thalès en mathématiques ?

Principalement à calculer des distances.

Pour pouvoir appliquer la réciproque du théorème de thalès, il faut s'assurer que deux séries de 3 points sont alignés dans le même ordre.

💪 tu veux devenir solide en maths ?

La réciproque du théorème de thalès.

La réciproque du théorème de thalès permet de montrer apres des calculs que des droites sont parallèles.

Réciproque du théorème de thalès :

Si on a ${ad}/{ae}={ab}/{ac}$ et si les points a, b, c et a, d, e sont alignés dans le même ordre alors (db) et (ec) sont parallèles.

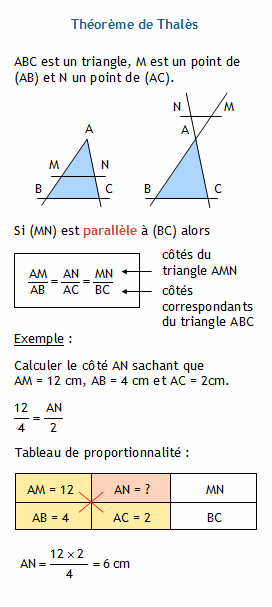
Soient un triangle abc, m un point de (ab) et n un point de (ac).

17 mai 2010 ∙ 2 minutes de lecture

Le théorème de thalès permet également de montrer que deux droites ne sont pas parallèles.

Les droites (mb) et (nc) sont sécantes en a.

Les points m, a et b sont dans le même ordre que les points n, a et c.

D’après la réiproque du théorème de thalès, on en déduit que les droites bc et mn sont parallèles.

Pour appliquer le théorème réciproque, il faut vérifier l’alignement des points dans le même ordre.

La réciproque de thalès sert à prouver que des droites sont parallèles conséquence :

A quoi sert ce théorème ?

Ce théorème sert à montrer que deux droites sont parallèles.

Exemple d’application de la réciproque du théorème de thalès exemple :

Ac = 10 cm ae = 4 cm ad = 6 cm ab = 15 cm montrer que les droites (ed) et (bc) sont parallèles.

Et si les points a, b, c et a, d, e sont alignés dans le même ordre alors (db) et (ec) sont parallèles.

Vous ne pourrez parler de réciproque du théorème de thalès qu'après avoir calculé les deux fractions (travaillez en valeur exactes!!).

Pour montrer que deux fractions sont égales il faut.

Si les points a, b et m sont alignés;

Les points a, c et n sont alignés;

Les droites (bc) et (mn) sont parallèles, alors d’après le théorème de

Doc a. garland p1/3 collège jules ferry de neuves maisons 3ème:

La réciproque du théorème de thalès 1.

L'énoncé 2 deux exemples types.

Abc est un triangle tel que ab=7cm ;

M est un point de [ab] tel que am=2,8cm.

A quoi ça sert ?

Vérifier que deux droites sont ou ne sont pas parallèles.

La réciproque du théorème de thalès sert donc à démontrer que 2 droites sont parallèles.

Chaque hypothèse est importante.

Le théorème de thalès permet de calculer des distances dans une configuration géométrique comportant des droites parallèles.

La réciproque du théorème de thalès sert à démontrer que deux droites sont parallèles en calculant des rapports de distances.

3. 1 enoncé de la réciproque.

Soient deux droites (ab) et (ac) sécantes en a.

Soit d un point de la droite (ab) distinct de a, et e un point de la droite (ac) distinct de a.

Si les points a, b et d d’une part, et a, c et e d’autre part sont alignés dans le même ordre.

Je vous présente le théorème de thalès et réciproque avec des exercices corrigés.

Soient deux droites (d 1) et (d 2) sécantes en a.

Soient deux points b et m de la droite (d 1) distincts de a.

Soient deux points c et n de la droite (d 2) distincts de a.

Si les droites (bc) et (mn) sont parallèles alors on a :

Réciproque du théorème de thalès.

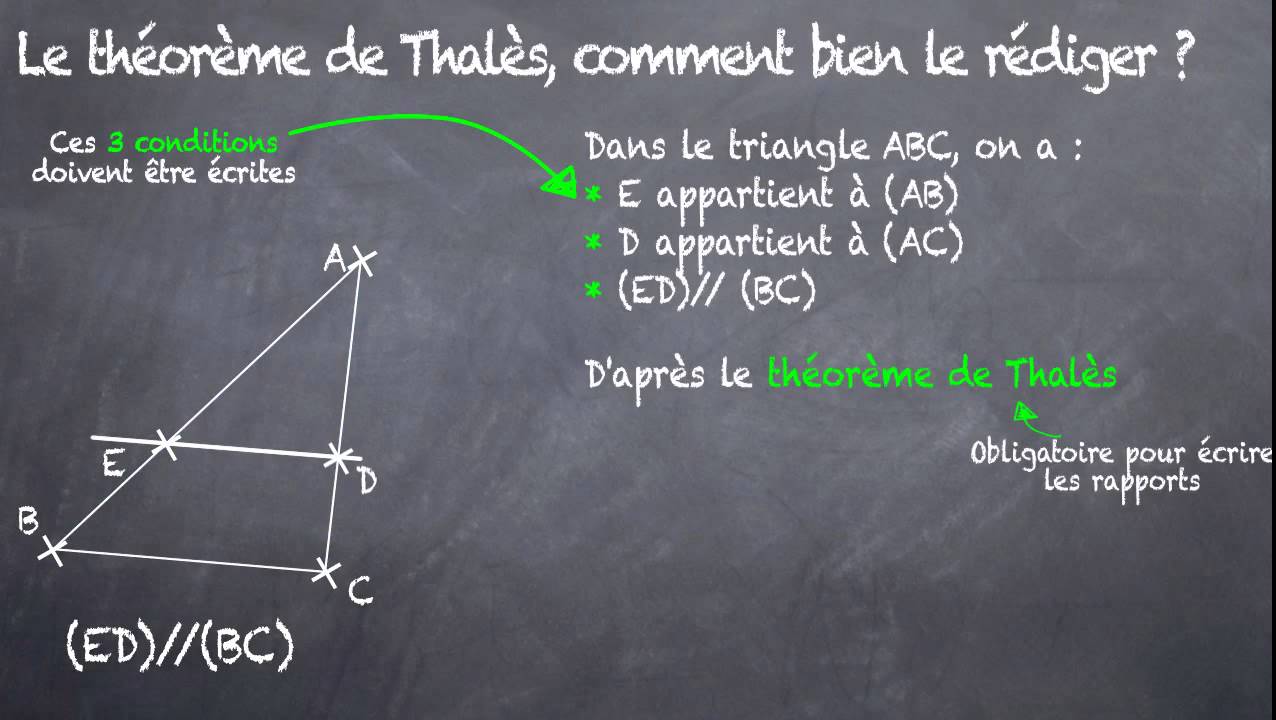
Considérons un triangle abc.

Si une droite coupe \left ( ab \right) en m et \left ( ac \right) en n, telle que :

Les points a, m, b et a, n, c sont dans le même ordre.

Alors les droites \left ( mn \right) et \left ( bc \right) sont parallèles.

On veut démontrer que les droites \left ( mn \right) et.

J’utilise la réciproque du théorème de thalès et donc (ab)//(de).

Donc on ne peut pas utiliser la réciproque du théorème de thalès.

(pr) et (de) ne sont pas parallèles.

Exercices conseillés en devoir p239 n°7 à.