C Est Quoi L Aire D Un Triangle

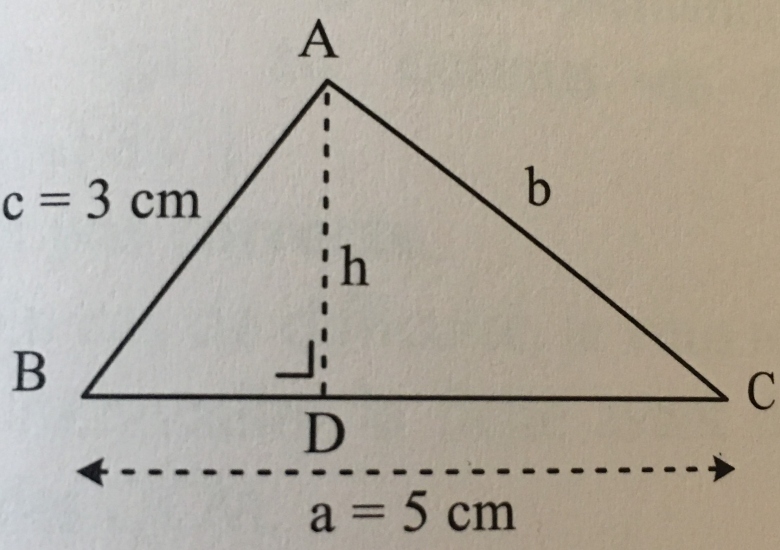
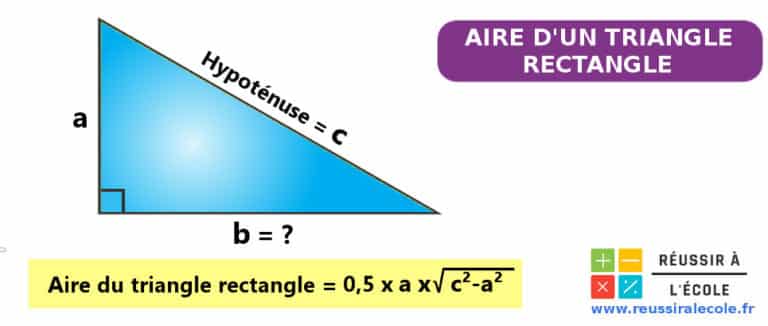
Dans le cas d’un triangle rectangle, la base b correspond à l’hypoténuse, et la hauteur h provient toujours de l’angle droit comme dans le schéma suivant.

Une aire en c m 2 cm ^ 2 cm2.

B la base d’un triangle rectangle ou la longueur de l’hypoténuse en cm.

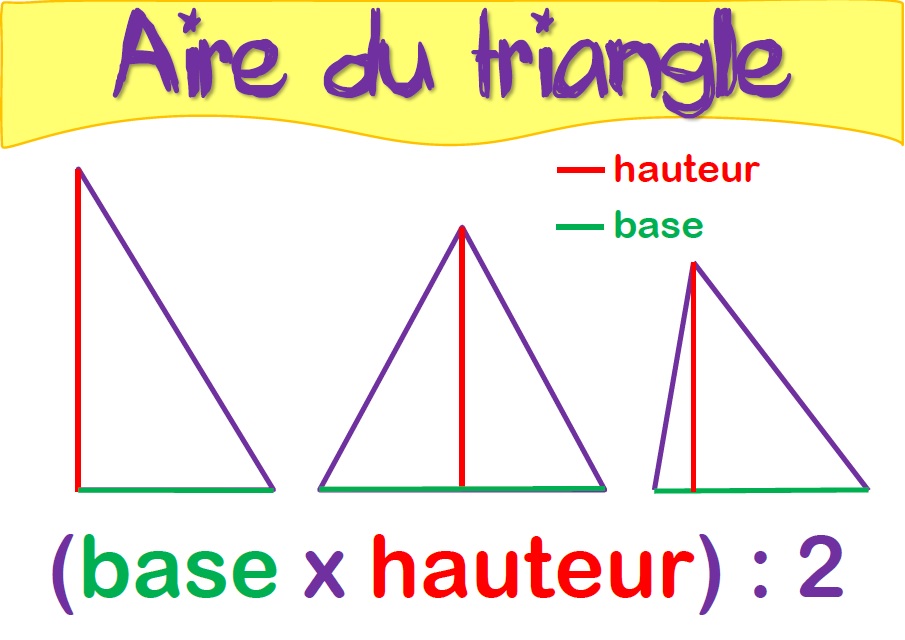
Dans le cas d'un triangle rectangle, les côtés adjacents à l'angle droits constituent une base et sa hauteur.

Par conséquent, pour calculer l'aire d'un triangle rectangle, il faut multiplier les longueurs des deux côtés adjacents à l'angle droit et diviser le résultat par 2.

Aire du triangle = base x hauteur / 2 = b. c / 2 exemple :

Dans le « triangle persan », la turquie incarne précisément un allié à part.

Son appartenance à l'otan pourrait la placer d'emblée dans le.

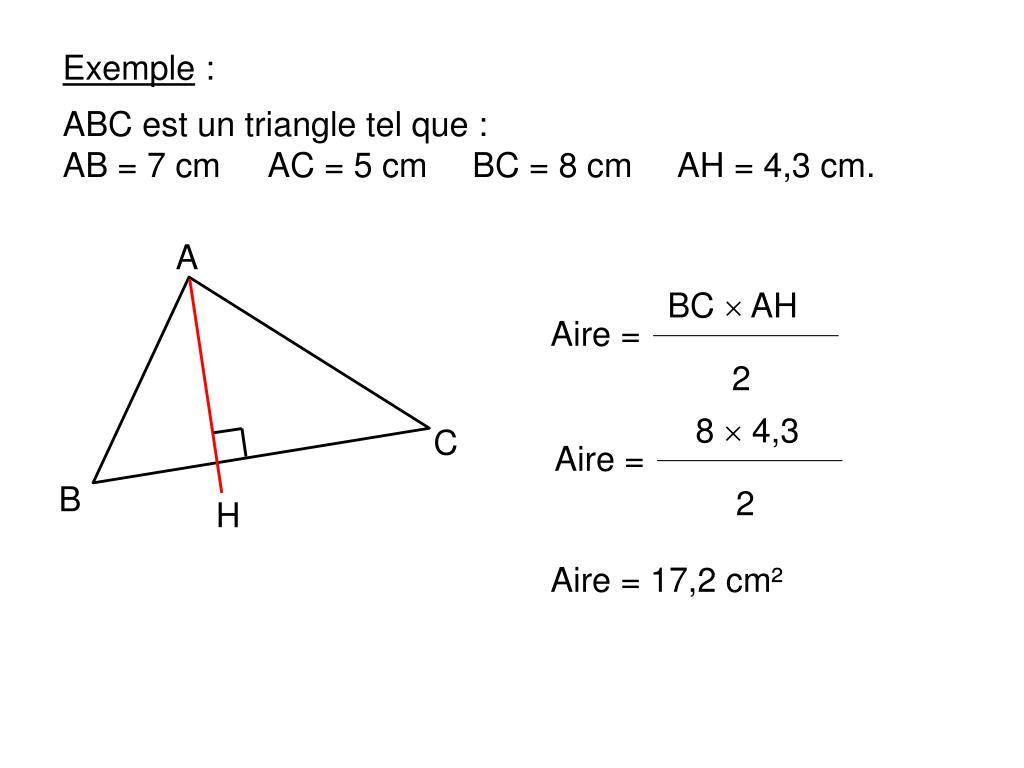
Si c désigne la longueur d'un côté d'un triangle et h la hauteur relative à ce côté, l'aire de ce triangle est égale à (c × h) ÷ 2.

Aire du triangle quelconque abc :

(ah) est la hauteur relative à [bc].

Bc = 5 cm ;

Ah = 4 cm.

L'aire du triangle abc, en cm 2, est égale à :

On obtient la même aire en calculant :

Aire du triangle abc rectangle en a :

(ab) est la hauteur.

If you're seeing this message, it means we're having trouble loading external resources on our website.

Si vous avez un filtre web, veuillez vous.

Créé par sal khan.

Google classroom facebook twitter email trier par :

Le plus voté conseils et remerciements

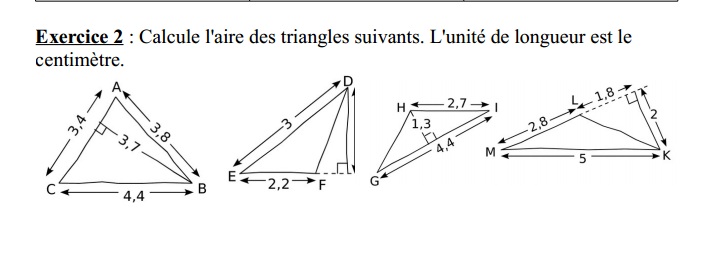
On peut calculer l'aire d'un triangle en connaissant les mesures de ses trois côtés.

Cette formule est très pratique dans la réalité si l'on veut calculer l'aire d'un triangle sans avoir comme donnée la hauteur ou si le triangle n'est pas particulier.

Aire du triangle = formule appelé aussi formule de heron.

Quelle est l’aire de la surface d’un triangle qui à 24 m de base et 8 m de hauteur.

S = = = 96 m 2.

Aire des triangles partic uliers:

· triangle r ect a n g le · triangle is o c è l e · trian g le équ i latérale.

Aire de triangles de même base et de même hauteur :

Aire d’un triangle isocèle aire d’un triangle équilatéral l’aire d’un triangle quelconque peut être calculée sans connaître sa hauteur à partir de la formule de héron (du nom du mathématicien grec héron d’alexandrie) ou de la loi des sinus.

Soit un triangle quelconque défini par trois points a,.