C Est Quoi La Hauteur D Un Triangle

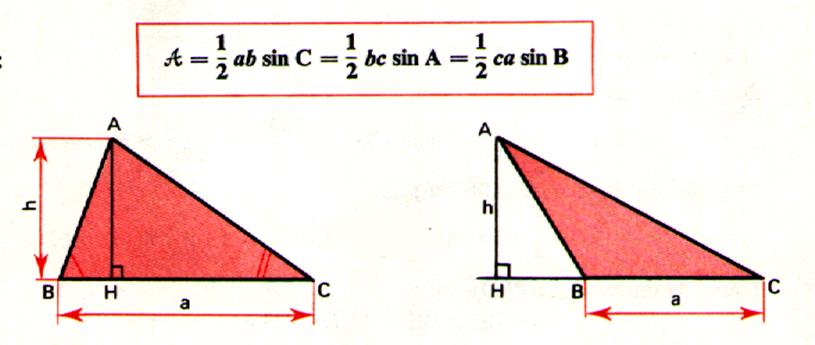
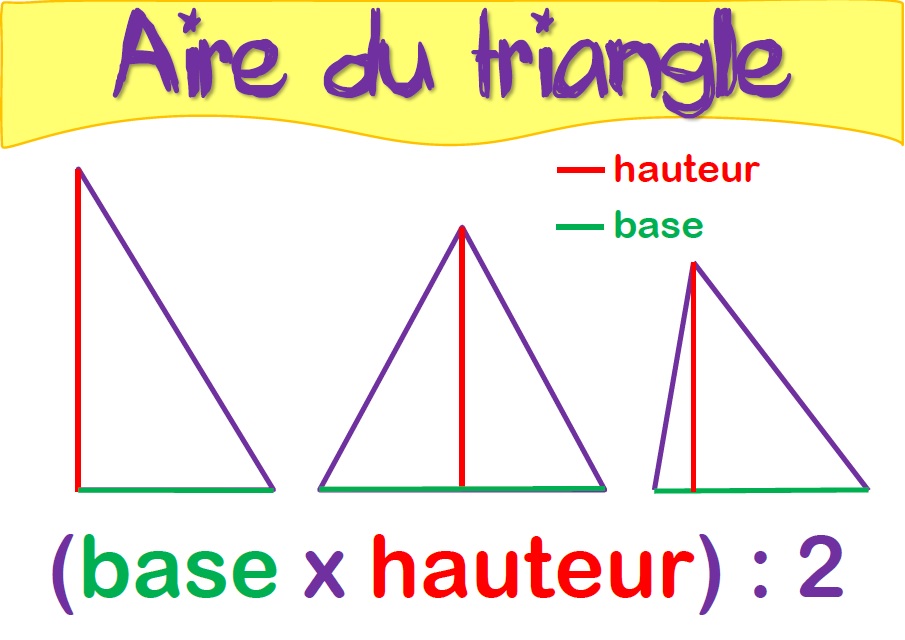
La formule la plus courante est la suivante :

[1] , formule dans laquelle :

A {\displaystyle a} est l'aire du triangle ;

B {\displaystyle b} est la longueur de la base du triangle ;

H {\displaystyle h} est la hauteur associée à la base précédente.

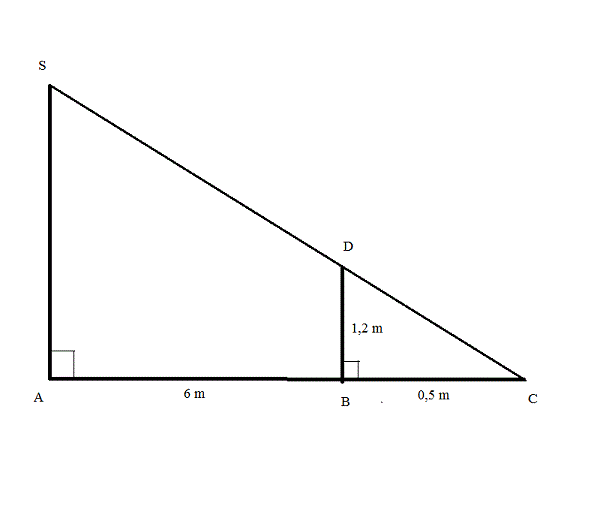
Observez votre triangle et.

Les hauteurs dans les triangles.

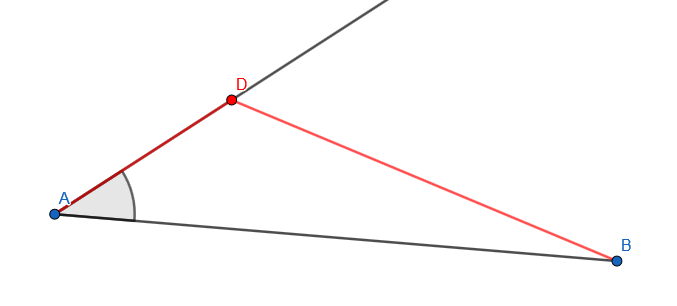
Dans un triangle rectangle, on appelle hauteur une droite qui passe par un sommet et qui est perpendiculaire au côté opposé.

Dans la figure, on dit que p est le pied de la.

29 août 2007 ∙ 1 minute de lecture.

Le point i milieu de [bc] a pour image le point a qui est donc le milieu de [b'c'].

La hauteur issue de a est perpendiculaire à [bc] donc est perpendiculaire à [b'c'] et passe par son milieu.

C'est la médiatrice du segment [b'c'].

On démontre ainsi que les trois hauteurs du triangle abc sont les trois médiatrices du triangle a'b'c'.

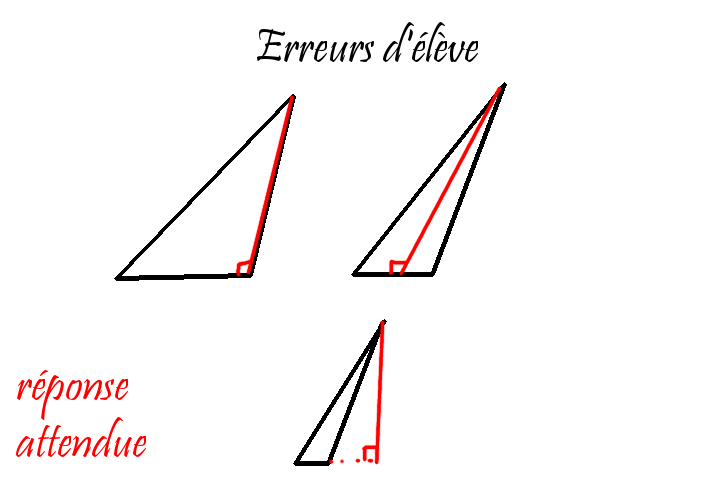
La hauteur d'un triangle est la droite passant par un des trois sommets et orthogonale à la droite qui supporte le segment opposé.

Il y a donc trois hauteurs dans un triangle.

Les trois hauteurs s'intersectent en un point remarquable, appelé l' orthocentre.

Dans un triangle abc, il existe une unique droite passant par le sommet a et.

Hauteurs dans un triangle mathématiques.

Hauteurs dans un triangle.

Dans cette leçon, nous allons apprendre à identifier les hauteurs d'un triangle et à utiliser leurs propriétés pour déterminer une longueur manquante.

Déposer un côté de l'angle droit de l'équerre sur la base du triangle.

Aligner l'autre côté de l'angle droit de l'équerre avec le sommet du triangle.

Tracer le segment qui part du sommet et qui rejoint perpendiculairement la base du triangle.

Ce segment est la hauteur du triangle.

About press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new features press copyright contact us creators.

Dans un triangle rectangle, la hauteur issue de l’angle droit découpe ce triangle en deux triangles semblables entre eux et semblables avec le triangle d’origine.

Dans le triangle ahc, on a.

Dans le triangle abc, on a.

Dans le triangle abc, on a aussi.

C'est en effet également possible de savoir comment calculer une aire d'un triangle équilatéral même si vous n'avez pas la hauteur.

Pour cela, retenez bien cette formule :

Racine carrée de 3 divisée par 4 x le côté au carré = votre aire.

Chaque triangle a alors trois hauteurs, chacune par rapport à chacun de ses côtés.

Les hauteurs du triangle se coupent à l.

Cours sur “les hauteurs d’un triangle” pour la 6ème.

La notion de hauteur est importante car cela nous permettra, dans le chapitre 16, de calculer l’aire d’un triangle.

Dans un triangle, la hauteur issue d’un sommet est la droite qui passe par ce sommet et qui coupe perpendiculairement le côté opposé à ce sommet.

Le périmètre d'un triangle s'obtient en additionnant les trois côtés.

La hauteur est une droite qui passe par un sommet et qui est perpendiculaire au côté opposé (la base ).

J'utilise la hauteur pour calculer l' aire d'un triangle :

(hauteur x base) ÷ 2

La formule de l’aire latérale d’un cône, l, est = , l où est le rayon de la base du cône et est la génératrice.

C’est quoi la hauteur d’un triangle?

La hauteur d’un triangle est une droite qui passe par un sommet du triangle et qui est perpendiculaire au côté opposé à ce sommet.

Pour construire une hauteur, il te faut une.

La première chose à faire pour calculer la hauteur d'un triangle consiste à écrire le théorème de pythagore, c 2 = a 2 + b 2, où c est l'hypoténuse (le côté opposé à l'angle droit).

Cours sur “les hauteurs d’un triangle” pour la 5ème.

La hauteur issue d’un sommet dans un triangle est la droite passant par ce sommet et perpendiculaire au côté opposé.

Il faut parfois prolonger le côté [bc] pour pouvoir tracer la hauteur issue de a.

On place un côté de l.