Le calculateur calcule les paramètres d'un cône circulaire droit ou du développement d'un cône circulaire tronqué droit.
Nous avons le rayon de la base inférieure, le raton de la base supérieure (dans le cas de cône tronqué) et la hauteur du cône.
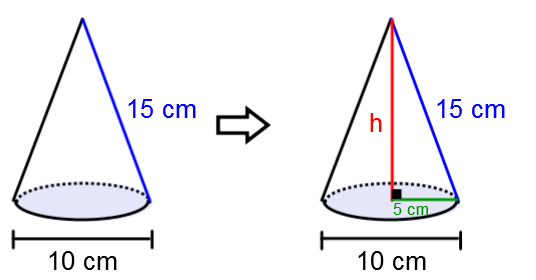
Nous devons trouver la longueur du côté.
Vous obtenez alors l’aire totale de surface du cône, en unités carrées.
At = 157 + 78, 5 = 235, 5 {\displaystyle {\text {at}}=157+78,5=235,5} ainsi, l’aire totale de la surface d'un cône ayant 5 cm de rayon et une génératrice de 10 cm est de 235,5 cm 2.
Le rayon d'un cône est le rayon de sa base circulaire.
Vous pouvez trouver un rayon à travers son volume et sa hauteur.
Multipliez le volume par 3.
Par exemple, le volume est 20.
La multiplication de 20 par 3 est égale à 60.
Multipliez la hauteur par π, qui est une constante numérique qui commence à 3,14 et ne se termine jamais.
Calcul rayon de la base d'un cône.
Kikou, la formule du cone de révolution c'est.
V= (aire de la base*hauteur)/3.
Pour trouver la longueur du rayon, il faut prendre la formule à l'envers:
Essaies de faire les cacul, tu devras trouver 6cm.
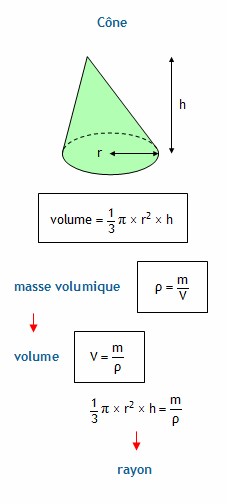
Le volume des cônes.
Malgré que les cônes soient des corps ronds, la façon de calculer leur volume est la même que celle des pyramides à la différence près que l’ aire de la base sera toujours celle d’un disque.
Afin de déterminer l'espace en 3 dimensions qu'un cône occupe, on considère d'abord l'aire de sa base.
Pour calculer la longueur de la génératrice d’un cône, son rayon et sa hauteur doivent être exprimés dans la même unité de longueur.
Le résultat du calcul de la longueur de la génératrice du cône sera exprimé dans cette même unité.
La génératrice d’un cône est parfois appelée à tort « côté du cône ».
Un cône de révolution est constitué d'une base en forme de disque et d'une surface conique.
On appelle hauteur du cône de révolution, le segment perpendiculaire à la base issu du sommet.
Le rayon d'un cône de révolution est le rayon de la base.
On peut générer le cône en faisant tourner un triangle rectangle autour de la hauteur.
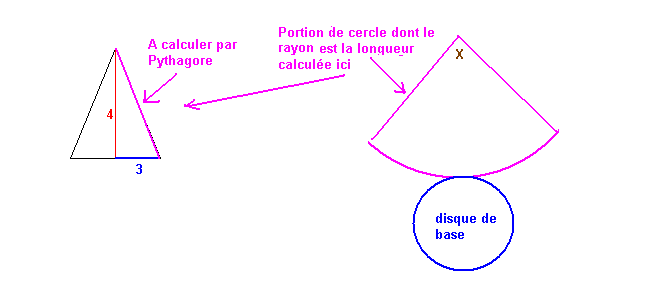
Calcul du rayon et de l'angle au centre du patron d'un cône circulaire droit.
Entrer les valeurs voulues dans les cases entourées en rouge (utiliser un point à la place de la virgule) et appuyer sur le bouton recalculer 1°) si on connaît le.
La base d'un cône est formée d'un disque.
La formule permettant de calculer l'aire de ce disque est la suivante.
Ab = πr2 a b = π r 2 où ab:
Aire de la base r:
Aire de la base r:
Lorsqu’on a la mesure du rayon, on applique cette formule.
Travailler sur un cône de révolution.
Lorsqu'on fait tourner le triangle rectangle oab autour de [oa], on obtient un cône de hauteur oa et de génératrice ab.
Ob est le rayon du disque de base.
Si on appelle r le rayon du disque de base, h la hauteur et g la génératrice du cône.
G2 = h2 + r2.
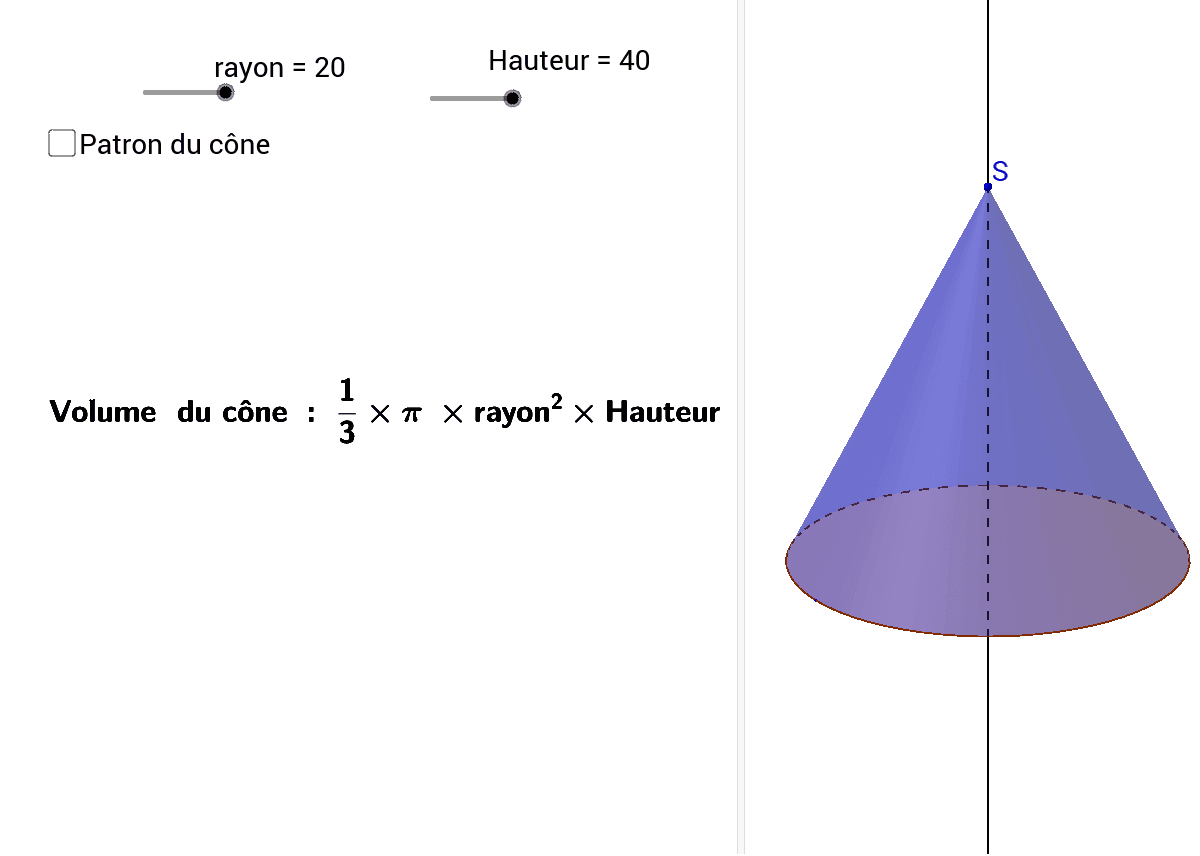
V = × π × r2 × h.
Calculer le volume d'un cône.
Le volume d'un cône de révolution est égal à un tiers de l’aire de sa base multipliée par la hauteur du cône h.
Si la base d'un cône est un disque de rayon r son aire est égale à :
Alors la formule du volume du cône est égal à :
Π × r 2 × h ÷ 3 ou encore :
* entrer les valeurs dans la.
Chacun des quatre secteurs égaux que l'on peut découper dans ce disque a un arc de 32.
Si l'on fabrique un cône avec ce secteur il aura une génératrice de 16 cm et une circonférence de la base égale à 8.
Pour en calculer la surface, il est indispensable de connaître le rayon de la base et la hauteur prise perpendiculairement à la base.
Il existe plusieurs formules pour calculer la surface d’un cône selon les données dont vous disposez.
L’on additionne notamment l’aire de la surface latérale à l’aire de la surface de base.
Calculer le rayon r de la base d'un cône connaissant son volume et sa hauteur h.
Relation entre le volume du cylindre et le volume du cône ayant le même rayon et la même hauteur.
Taper 0. 65 au lieu de 0,65 (indiquer le 0 avant le point).
Taper vos données pour calculer l'échelle de la réduction du grand cône.
En déduire le rayon et l'aire de la section, le volume du petit cône.
Un cône de révolution est un solide obtenu en faisant tourner un triangle rectangle autour d’un des côtés de l’angle droit.
[as] est une génératrice du cône.
On pose as = l.
Un cône a un rayon de 3 cm et une hauteur de 4.
Si vous connaissez le volume v et la hauteur du cône h, exprimez son rayon de base r à partir de la formule v = 1/3 ∙ πr²h.
R² = 3v / πh, d'où r = √ (3v / πh).
Si vous connaissez l'aire de la surface latérale du cône s et la longueur de sa génératrice l, exprimez le rayon r à partir de la formule: