Déterminer les coordonnées d'un point pour qu'il y ait un parallélogramme;
Démontrer la colinéarité de deux vecteurs;
Déterminer les coordonnées d'un point pour respecter la colinéarité;
Montrer que trois points sont alignés en utilisant les coordonnées;
Montrer que deux droites.
Utiliser les vecteurs pour démontrer que 3 points sont alignés.
Bonjour à tous, à toutes !!
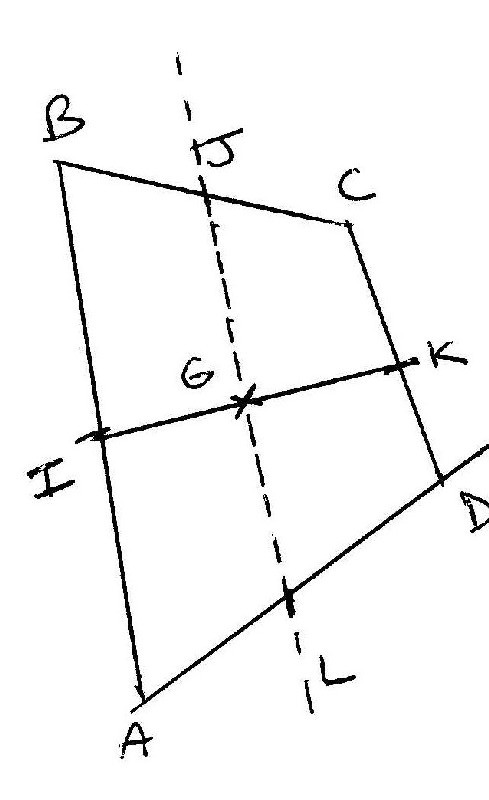
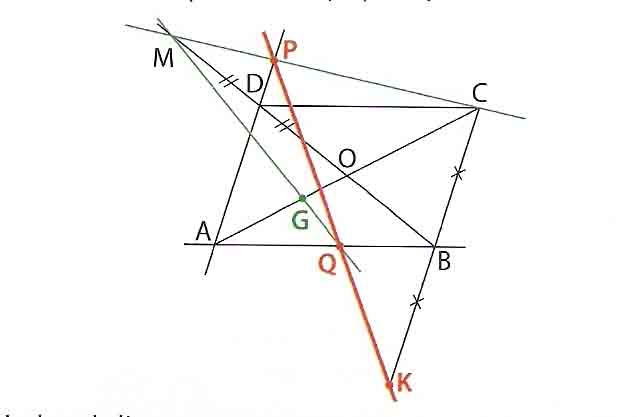
Abc est un triangle quelconque.
I est le milieu de [ab] j est le milieu de [ac] k est le milieu de [bc] on note l.
Deuxième partie géométrie analytique.
Coordonnées des vecteurs dans une base orthonormée.
Les points m m m, n n n et p p p sont alignés si,.
→ cb c b →, ce qui revient au même) sont colinéaires.
En effet, deux vecteurs colinéaires ayant un point commun sont les vecteurs directeurs d’une même droite.
2 deux droites parallèles sont représentées par deux droites parallèles.
Deux droites sécantes sont représentées par deux droites sécantes 3 des points alignés dans un certain ordre sont représentés alignés dans le même ordre 4 il y a conservation des rapports de longueur sur un segment ainsi que sur des segments parallèles.
Les deux techniques pour montrer la colinéarité et que 3 points sont alignés.
Vérifier la colinéarité de deux vecteurs dans le repère.
Char snipeur 1 328.
3 points, égale deux vecteurs.
Si ils sont aligné, le produit scalaire est égale au produit des distances, et le produit vectoriel vaut 0.
3 points en combien de dimensions ?
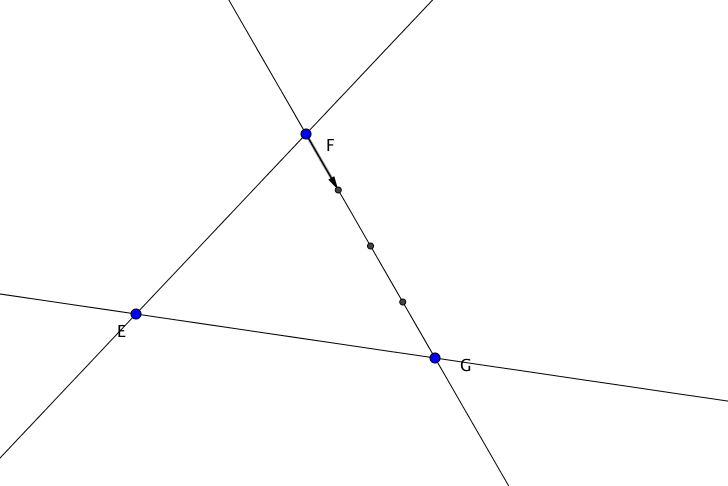
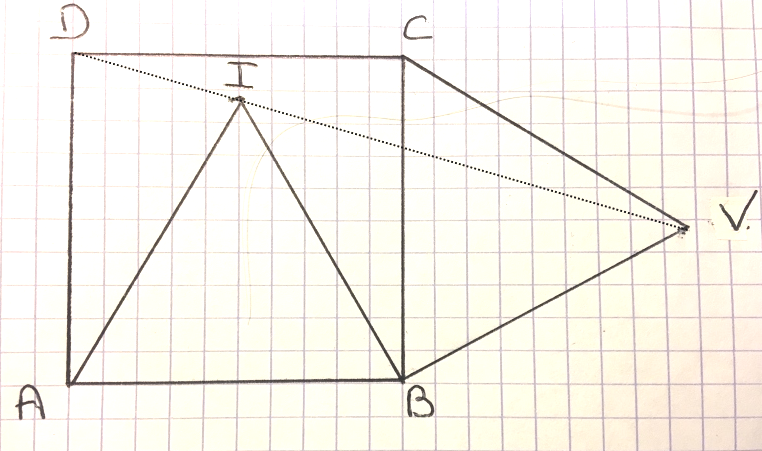
Soit e et f les points définis par:
Be*=1/2ab* et af*= 3ad* démontrer que les points c, e, f sont alignés.
(le * signifie vecteur) j'ai essayé de prouver que ce* et cf* sont colinéaires, mais sans succès.
Je vous remercie d'avance.
Bonjour, pour démontrer que des vecteurs sont colinéaires, on applique le cours :
Dans le repère (o, , ) :
Soit vecteur ayant pour coordonnées (x ;
Y) soit vecteur ayant pour coordonnées (x' ;
Y') les vecteurs et sont colinéaires si et seulement si.
Je définis la colinéarité des vecteurs et par la.
Message whatsapp au 07 67 45 85 81 en précisant votre nom d'utilisateur.
Étudier l’alignement de trois points dans le plan à l’aide d’un algorithme.
Les points a , b et c sont alignés ⇔ (ab) et (ac) ont le même cœfficient directeur.
Les points a , b et c sont alignés ⇔ (ab) et (ac) ont des vecteurs directeurs colinéaires ⇔ le déterminant des vecteurs et est nul.
Les points a , b et c sont.
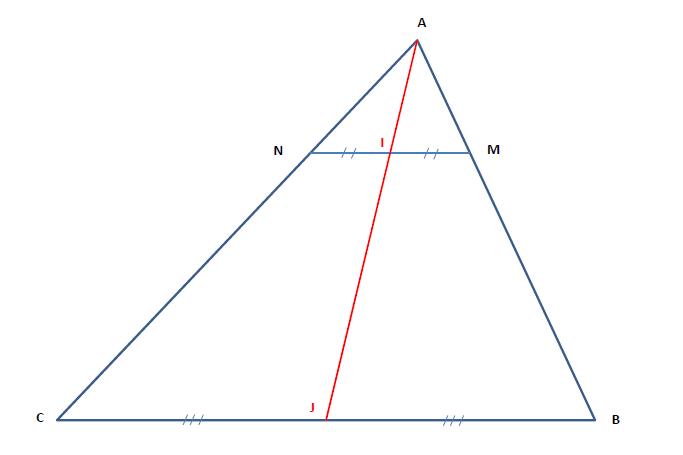
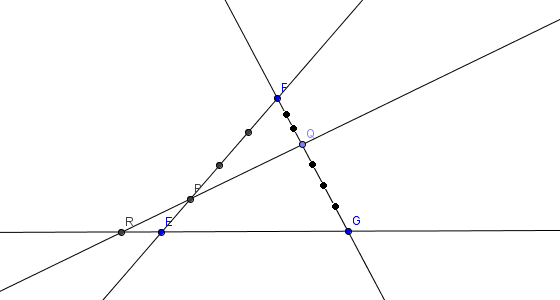
Les points n et p sont tels que :
→ an = (3 / 2) → ab + → ac et → bp = (2 / 5) → bc.
1) faire une figure.
2) calculer les coordonnées de n et p.
3) montrer que les points a, n et p sont alignés.
Bon courage, sylvain jeuland.
Comment montrer que 3 points a, b et c sont alignés en passant par l’équation cartésienne ?
Pour le démontrer ici, on partira des points a et b, pour définir une équation de la droite (ab).
Pour définir l’équation cartésienne d’une droite d, on a besoin d’un point de passage et d’un vecteur directeur.
En isolant « c » on.
Ce que tu cherches, c'est à prouver que a, m et n sont alignés.
Tu cherches donc à montrer que deux vecteurs, faisant intervenir ces trois points, sont colinéaires.
En l'occurrence là tu as fait apparaître am dans la 1ère équation, et tu as déjà an dans la seconde.
Ce que tu cherches donc à montrer c'est que am = k an où k est un.
Si trois points a b et c sont tels que l'angle abc est nul, alors les points a b et c sont alignés.
Si deux droites parallèles ont un point commun, alors elles sont confondues.