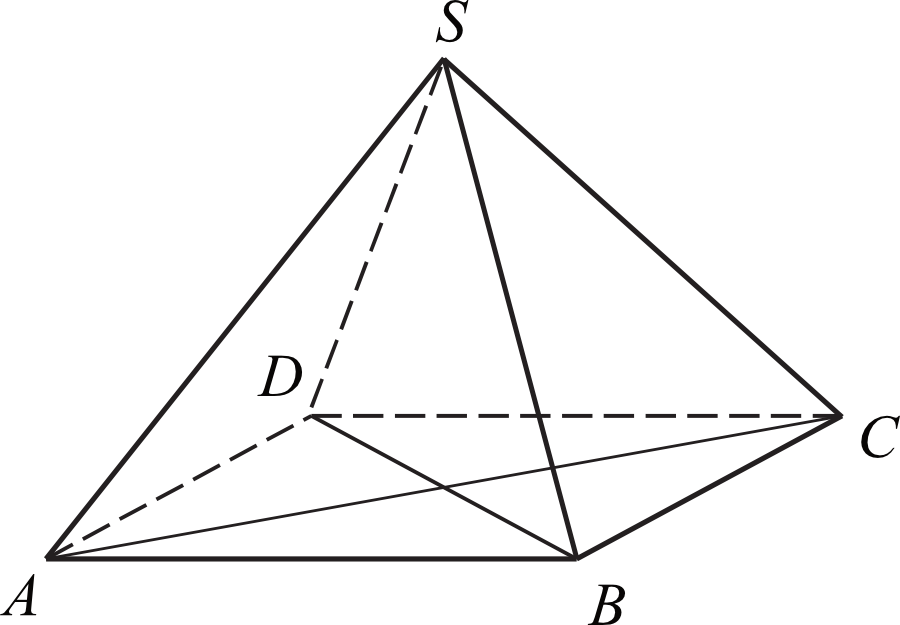
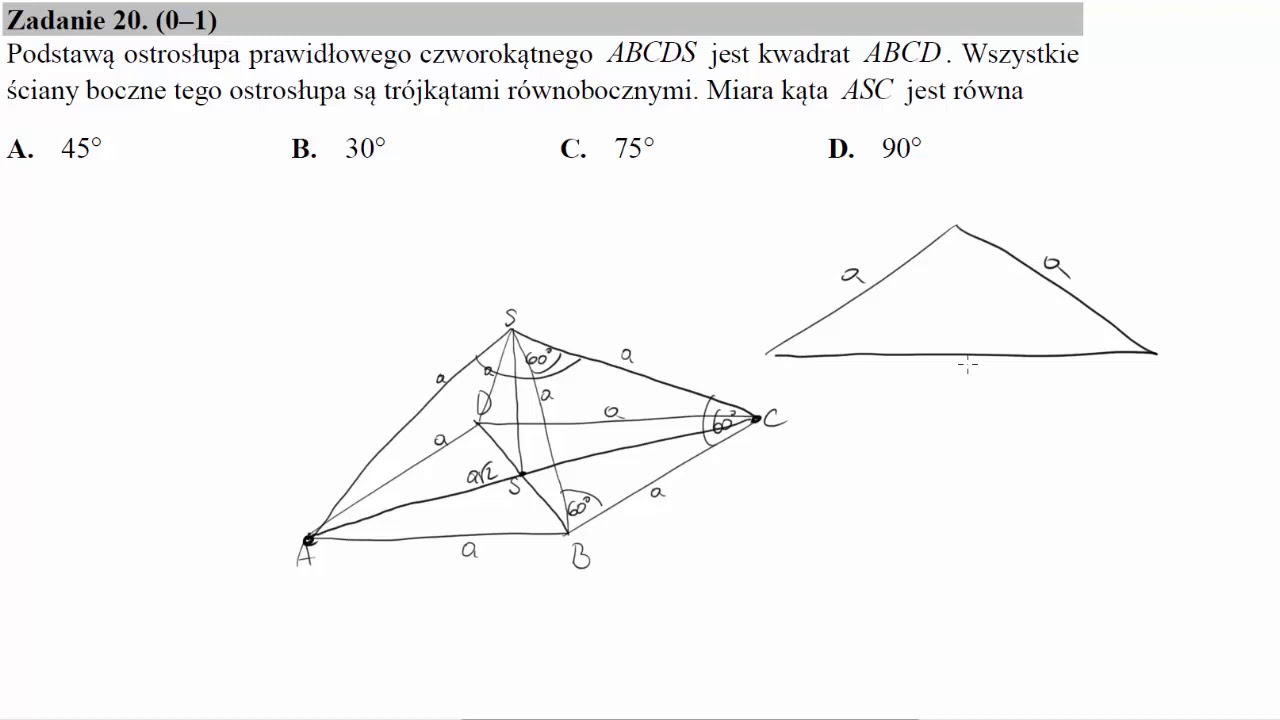
Zadanie: zadanie 101 podstawą ostrosłupa prawidłowego czworokątnego abcds jest kwadrat abcd pole trójkąta równoramiennego acs jest równe 120 oraz ac as Rozwiązanie:.
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa : A. 5 B. 7 C. 8 D. 10 Pokaż rozwiązanie zadania Zadanie maturalne nr 20, matura 2014 Stożek i.
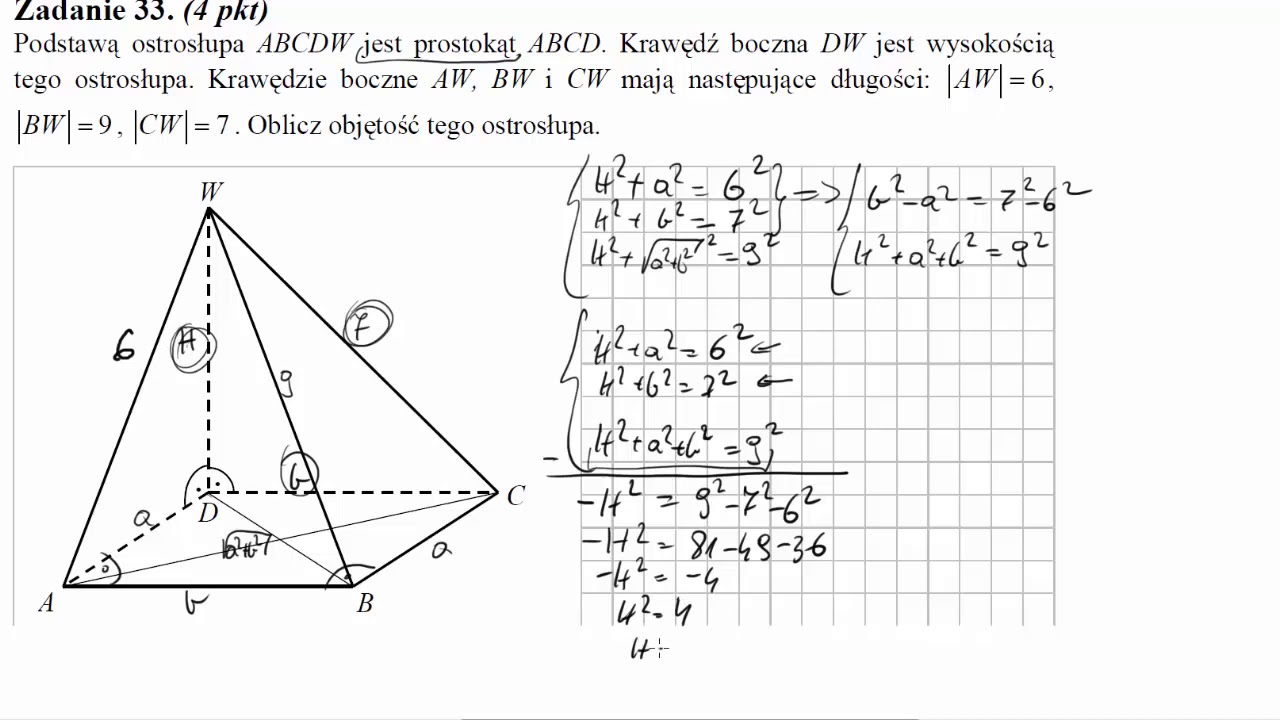
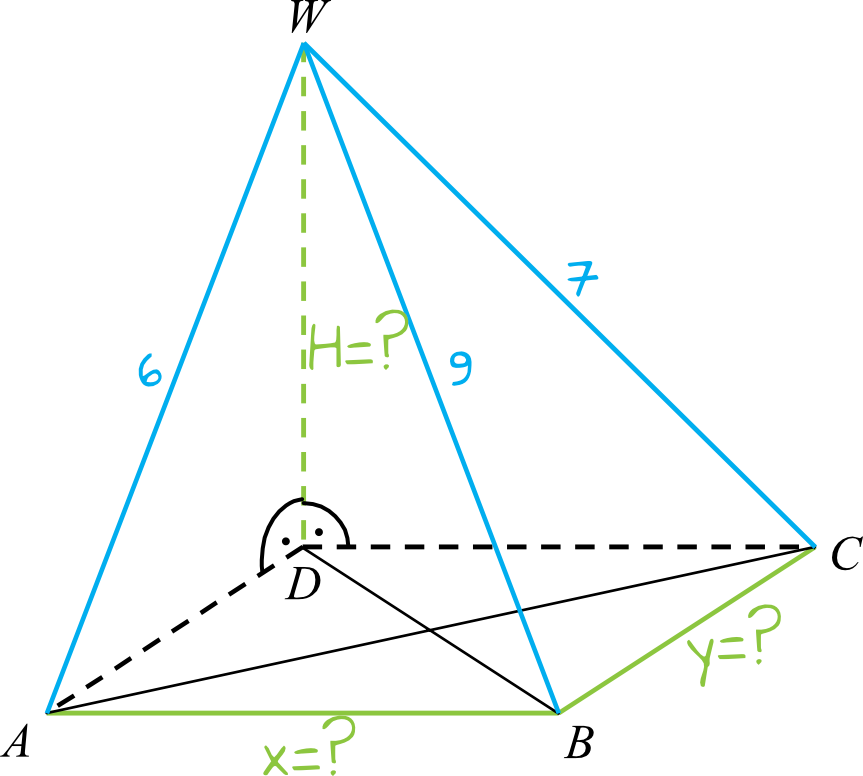
Oblicz objętość tego ostrosłupa, jeśli wiadomo, że |AB|=8 cm i |AF|= 5 cm. BŁAGAM! Cały czas wychodzi mi zły wynik xd. Question from @ZzzosiaaA - Szkoła podstawowa -.
Obecnie platforma Scholaris nie jest już wspierana a funkcję udostępniania materiałów edukacyjnych przejęła Zintegrowana Platforma Edukacyjna (ZPE), aby zapewnić.
Podstawą ostrosłupa ABCDS jest kwadrat ABCD o boku długości \(2 \sqrt{2} \).Krawędź boczna DS jest wysokością tego ostrosłupa, a jej długość jest równa 8.
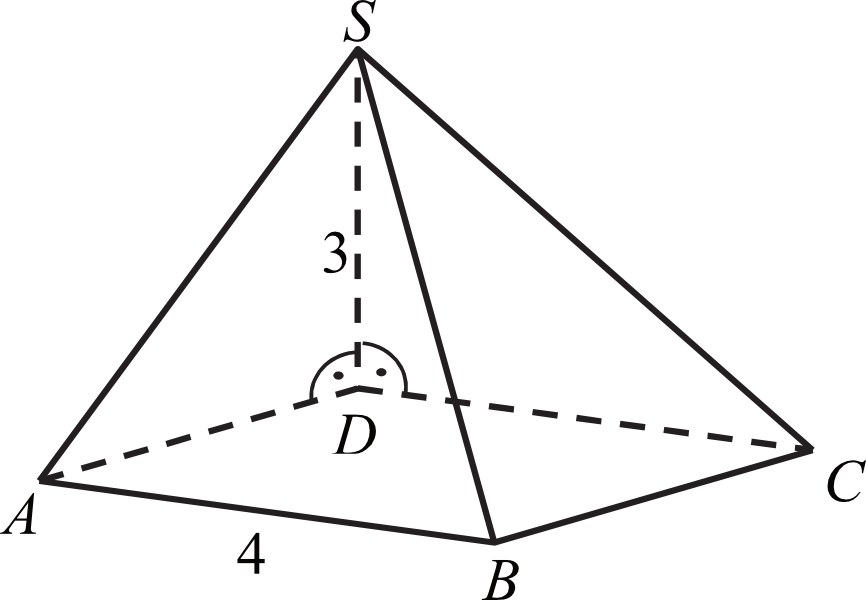
http://akademia-matematyki.edu.pl/ Podstawą ostrosłupa jest kwadrat ABCD o boku długości 4. Krawędź boczna DS jest prostopadła do podstawy i ma długość 3 (zo...
Podstawą Ostrosłupa Prawidłowego Czworokątnego Abcds Jest Kwadrat Abcd. Wszystkie ściany boczne tego ost. ... Objętość Graniastosłupa Prawidłowego.
5.176. Odcinek AB jest równoległy do płaszczyzny zz i ma długość 21 cm. Prosta k, przecinająca odcinek AB, jest prostopadła do płaszczyzny i przebija tę płaszczyznę w.
Podstawą ostrosłupa prawidłowego czworokątnego ABCDS jest kwadrat ABCD. Pole trójkąta równoramiennego ACS jest równe 120 oraz AC : AS = 10 :13 . Oblicz pole ...
Podstawa ostroslupa jest kwadrat abcd, zaś krawedz boczna sd jest jego wysokoscia. Source: www.youtube.com Long tail keywords (2 words) matematyka.
Krawędź boczna DS jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).Pole ściany BCS tego ostrosłupa jest równe A.20 B.10 C.16 D.12 Kategorie aa Bez kategorii ,.
Rozwiązanie zadania. Podstawą ostrosłupa prawidłowego czworokątnego ABCDS jest kwadrat ABCD. Wszystkie ściany boczne tego ostrosłupa są ...
Wysokość SE ściany bocznej ADS jest jednocześnie wysokością ostrosłupa, a punkt E jest środkiem krawędzi AD (zobacz rysunek). Pole ściany ADS jest równe 12 cm2, a objętość.
pole ostroslup to kwadrat wiec Ac to przekatna czyli boki kwadratu maj wymiar 10 bo D= a^2 w tymwypadku a= AC obliczamy h sciany bocznej 13^2*2=5*2+h*2.
Wiemy też, że ściany boczne są trójkątami równobocznymi. Możemy więc powiedzieć, że w takim razie wszystkie krawędzie tej bryły mają jednakową miarę i jest ona równa \(a\)..
Przekrój ostrosłupa płaszczyzną jest trapezem równoramiennym , gdzie i środki krawędzi i .Kąt między płaszczyzną , a płaszczyzną podstawy otrzymamy przecinając te.
Kwadrat ABCD jest podstawą ostroslupa ABCDF ,punkt E jest środkiem krawedzi AB , a odcinek EF jest wysokością ostrosłupa .Oblicz objętoć tego ostrosłupa ...
Zauważmy, że krawędź jest prostopadła do i do (bo jest równoległa do ).To oznacza, że krawędź jest prostopadła do płaszczyzny .Jest więc prostopadła do każdej prostej zawartej w tej płaszczyźnie, w szczególności trójkąt jest prostokątny.. Analogicznie wykazujemy,.
Na pierwszej ilustracji jest waga z 2 szalkami. Na lewej szalce jest położony odważnik 100dag, na drugiej szalce są 4 gruszki i odważnik 10dag. Na drugiej ilustracji.
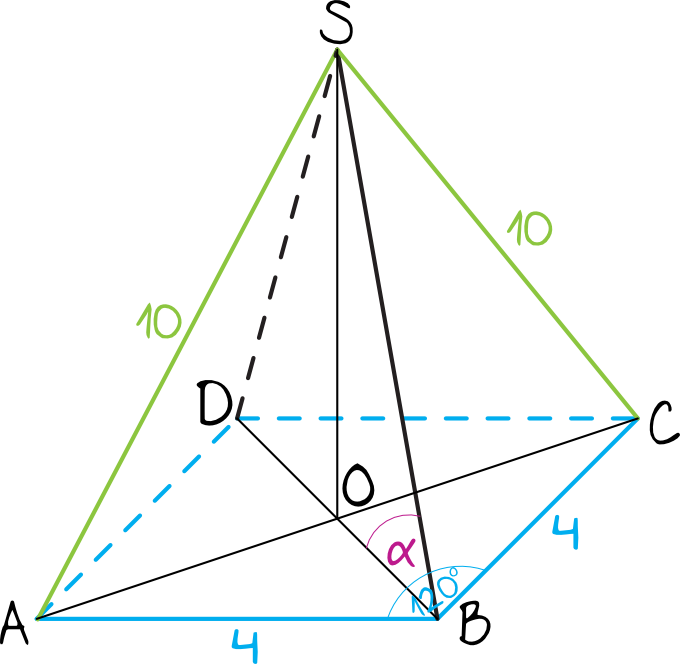
Krawędz boczna AS ma również długość a i jest prostopadła do płaszczyzny podstawy. Ostrosłup ten przecięto płaszczyną przechodzącą przez wierzchołek A i.
Podstawą Ostrosłupa Abcds Jest Kwadrat Abcd. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi abs i cbs., kwadrat w podstawie, 8636937.
Oblicz Objętość Ostrosłupa, Jeśliwiadomo, Że Ae=15,=17., Kwadrat W Podstawie, 8369842. Krawędź boczna sd jest wysokościąostrosłupa, a jej długość jest.
Pole Trójkątarównoramiennego Acs Jest Równe 120. (1pkt) podstawą ostrosłupa prawidłowego czworokątnego abcds jest kwadrat abcd (zobacz rysunek). W.
https://akademia-matematyki.edu.pl/ Podstawą ostrosłupa prawidłowego czworokątnego ABCDS jest kwadrat ABCD (zobacz rysunek). Wszystkie ściany boczne tego ost...