Où l'on démontre que racine de 2 ne peut pas être le quotient de deux entiers et que c'est donc un nombre irrationnel.
Et qui est que le nombre racine carrée de 2 est un nombre irrationnel alors il ya plusieurs manières de démontrer ce résultat mais la démonstration que je te propose aujourd'hui bien c'est probablement l'une des.
On a ainsi démontré que \(\sqrt{2}\) est irrationnel.
Démontrer que le produit de deux nombres rationnels est un nombre rationnel.
Trouver les diviseurs d'un nombre.
Retour vers la liste d'articles.
En remarquant que tout entier p est de la forme p = 3k ou p = 3k+1, ou encore p = 3k+2, montrer par l'absurde que 3 est irrationnel.
J'ai pensé à utiliser la manière habituelle, avec en gros p et q premiers entre eux mais finalement pas premiers entre eux et en y ajoutant une disjonction des cas.
Ça marche pour p=3k mais pas pour les 2.
On propose de démontrer que √2 est un irrationnel.
A désigne un entier naturel.
A) si a est pair, alors a² est pair ;
B) si a est impair, alors a² est impair.
Demonstration de l'irrationnalite de √2.
On utilise un raisonnement par l'absurde.
Nous appelons de tels nombres » irrationnels « , non pas parce qu’ils sont fous mais parce qu’ils ne peuvent pas être écrits comme un rapport (ou une fraction).
« la racine carrée de 2 est irrationnelle ».
On pense que c’est le premier nombre irrationnel jamais découvert.
Mais il y en a beaucoup d’autres.
De plus, un nombre entier est un cas particulier de nombre rationnel (avec 1 comme dénominateur).
Par exemple pour montrer que la racine carrée de 4 est rationnelle, il suffit de remarquer que 2 x 2 = 4, donc la racine carrée de 4 est égale à.
S’il est possible de trouver des entiers a, b qui vérifient cette égalité, on dit que p 2 estunnombrerationnel,sinononditque p 2 estunnombreirrationnel.
Lemme «pourtoutnombreentiera,sia2 estpair,alorsa estpair. » démonstration par contraposition :
Montrons que, si a est impair, alors a2 est impair.
Posonsa = 2n+1. alorsa 2= (2n+1)2 = 4n.
Tentons de démontrer que √2 est irrationnel, c’est à dire qu’il est impossible d’écrire √2 sous forme d’une fraction :
S u p p o s o n s q u e 2 s o i t u n n o m b r e r a t i o n n e l.
A l o r s i l e x i s t e a, b ∈ r t e l s q u e 2 = a b ( a v e c a b i r r e ˊ d u c t i b l e).
2 = a b ⇔ ( 2) ² = ( a b) ² ⇔ 2 = a.
Cours de mathématiques de seconde > racine carrée de 2 est irrationnel;
Racine carrée de 2 est irrationnel.
Le but de cette fiche est de démontrer que 2 \sqrt{2} 2 est irrationnel.
Démonstration des propriétés préalables.
Démontrons les propriétés préalables nécessaires à la suite de la démonstration :
Si a a a est pair, alors a.
Pour démontrer qu'un nombre est irrationnel, on raisonne par l'absurde.
On suppose que 2 est rationnel de la forme p/q (avec p et q premiers entre eux ) et on démontre que c'est impossible.
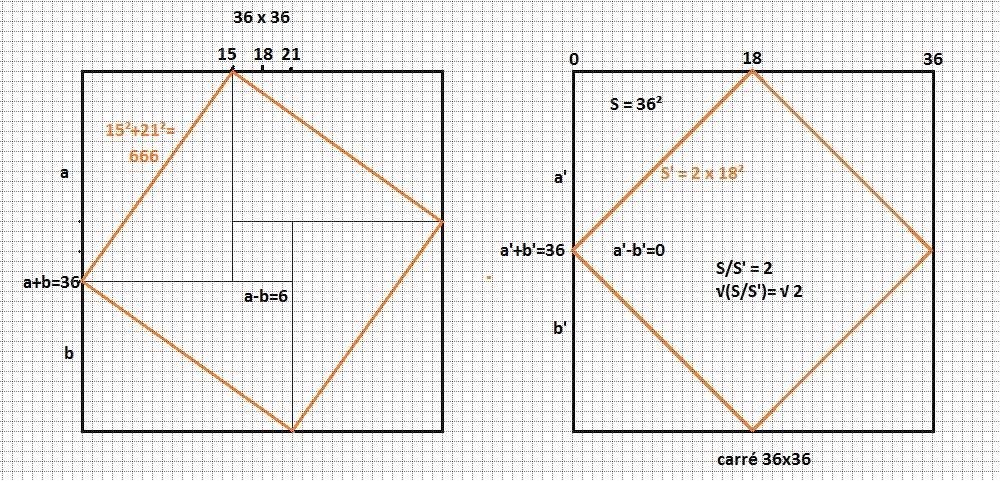
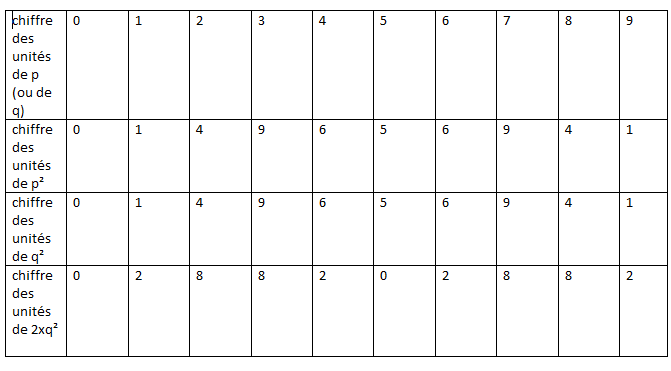
Si 2=p/q alors en élevant au carré on obtient 2=p²/q² soit p²=2q² et on compare le dernier chiffre de p² avec le dernier chiffre de 2q².
Démontrer que le nombre réel 2 est irrationnel.
Rappelons qu’un nombre x est dit irrationnel si et seulement si, x ne s’écrit pas sous la forme d’une fraction de deux nombres entiers relatifs.
Quels que soient les nombres relatifs a ∈ z, b ∈ n ∗ ( i. e.
X ≠ a b.
Mais de nombreuses autres fractions sont aussi égales à 1, 4, comme 28 20.
Mis sous forme de fraction irréductible, on obtient 7 5.
Ainsi, 2 divise à la fois p et q.
Cela contredit l’hypothèse initiale que p et q sont premiers entre eux.
Donc la racine de 2 est irrationnelle !
On peut montrer que la racine d’un nombre n qui n’est pas un carré parfait n’est pas rationnelle.
Pour rappel, un carré parfait n est un nombre tel qu’il existe k entier tel que n = k 2.
D'après le théorème de pythagore.
B 2 + b 2 = a 2 2 b 2 = a 2 2 = ( a b) 2 a b = 2.
S'il est possible de trouver des entiers a, b qui vérifient cette égalité, on dit que √ 2 est un nombre rationnel, sinon on dit que √ 2 est un nombre irrationnel.
Il te suffit de démontrer que racine de 6 est irrationnel.
Tu tritures un poil, dans un autre coin tu démontres que est irrationnel, et hop tu as ta démonstration complète.