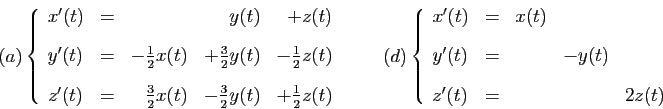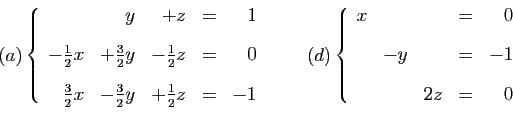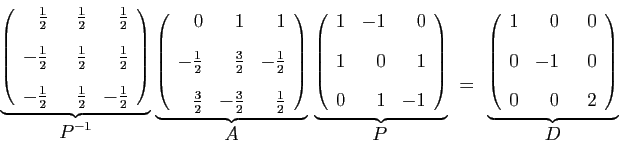Transcription de la vidéo.
Jusqu'ici on s'est intéressé à l'inversé des matrices de taille de 2 ou 3 3 mais on s'est même pas posé la question en fait est ce qu'il est possible d'inverser toutes les matrices carré de taille de deux de taille 3 3 ou de taille n est en fait la réponse c'est non toutes les matrices car ils ne peuvent pas.
Intuitivement, cela signifie que si l'on choisit au hasard une matrice carrée d'ordre n à coefficients réels, la probabilité pour qu'elle soit non inversible est égale à zéro.
La raison en est que les matrices non inversibles sont les racines (ou zéros) d'une fonction polynomiale donnée par.
En mathématiques et plus particulièrement en algèbre linéaire, une matrice carrée a d'ordre n est dite s'il existe une matrice b d'ordre n, appelée matrice inverse de a et notée :
B = a^−1 telle que :
Ab = ba = in si le déterminant d'une matrice a est non nul, alors a est inversible.
Si elles le sont, calculer leur inverse.
On calcule pour chaque matrice.
Pour la matrice a , donc la matrice a n’est pas inversible.
Pour la matrice b , donc la matrice b est inversible.
Pour la matrice c , donc la matrice c est inversible.
Maintenant que tu es un champion et que tu sais inverser une matrice, vient tester tes.
Tu souhaites en savoir plus sur la notion de matrice d'une application linéaire ?
Améliore tes connaissances sur cette notion grâce à notre article dédié au.
Est inversible si, et seulement si, ses coefficients diagonaux sont non nuls.
En transposant, on obtient un résultat similaire pour les matrices triangulaires.
Savoir inverser une matrice est nécessaire pour toute une gamme d’exercices sur ce sujet, en particulier lorsque l’on veut aborder la diagonalisation des matrices sereinement.
Si le déterminant d'une matrice a (à coefficients dans un corps commutatif) est non nul, alors a est inversible, son inverse étant donnée par :
= où t com(a) est la transposée de la comatrice de a. en effet (cf.
Article détaillé), toute matrice carrée a d'ordre n vérifie :
() = () = (). cette écriture permet un calcul aisé de l'inverse d'une matrice de petite dimension.
Soit a la matrice de f dans une base b.
A est inversible si et seulement si f est bijective.
Si p est une matrice de passage d’une base b 1 à une base b 2, alors p est inversible.
Une matrice carrée a est inversible si et seulement si rg (a)=n.
Soit a une matrice carrée telle.
Vérifier si une matrice est inversible.
M est inversible signifie que m admet un averse qu'on notera m⁻¹ tel que m*m⁻¹ = m⁻¹*m = i.
Si tu ne vois pas l'astuce, tu peux essayer de voir si ça marche pour m.
En algèbre linéaire, une matrice carrée n par n a est appelée inversible, s’il existe une matrice carrée n par n b telle que où ‘ in ‘ désigne la matrice identité n par n.
La matrice b est appelée matrice inverse de a.
Une matrice carrée est inversible si et seulement si son déterminant est non nul.
Une formule pour l’inverse d’une matrice carrée d’ordre {2} 2.
Il n’est pas toujours facile de voir au premier coup d’oeil si une matrice carrée {a} a est inversible ou non.
En revanche, c’est facile pour les matrices carrées d’ordre {2} 2 :
Proposition (inversibilité d'une matrice carrée d'ordre 2) soit {a=\begin {pmatrix}a.
Déterminer si une matrice est inversible notre mission :
Apporter un enseignement gratuit et de qualité à tout le monde, partout.
Plus de 4500 vidéos et des dizaines de milliers d'exercices interactifs sont disponibles du niveau primaire au niveau universitaire.