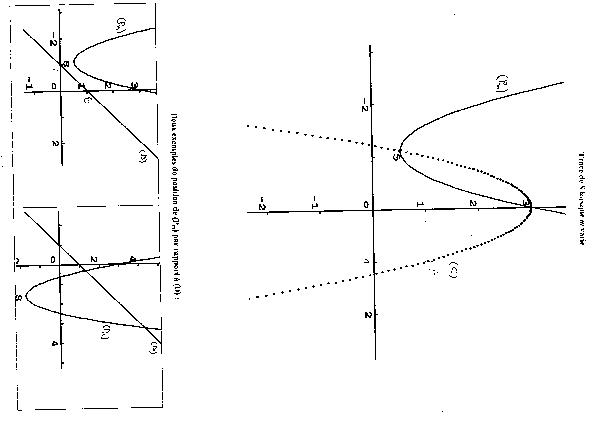
Trouver le foyer et la directrice d'une parabole à partir de son équation.
Déduire de la représentation graphique d'une ellipse les coordonnées de ses foyers.
Apporter un enseignement gratuit et de qualité à tout le monde, partout.
Plus de 4500 vidéos et des dizaines de milliers d'exercices interactifs sont disponibles du niveau primaire au niveau universitaire.
Inscription & aide gratuites.
Et après il faut trouver un point appartenant à la parabole (de coordonnées xa et ya par exemple) et il suffit de résoudre :
Donc si on augmente x de 1 à partir du sommet (;
) y augmente de :
La règle de la fonction est f(x) = 4, 5x2.
Trouve la règle de la fonction polynomiale de degré 2 qui passe par le point (1, 5;
Remplacer x et f(x) dans l’équation par les coordonnées d’un point.
F(x) = ax2 − 11, 25 = a(1, 5)2.
Isoler le paramètre a.
Équation fonction a partir d un graphique.
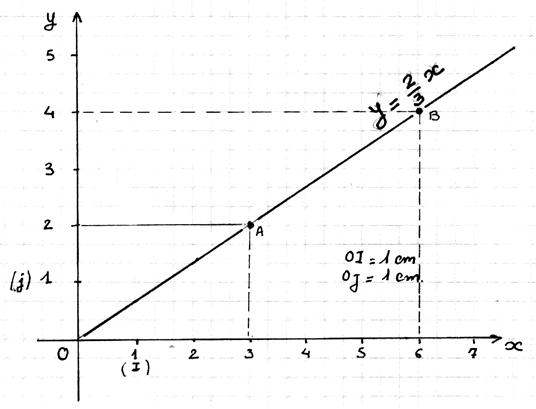
Une fonction affine c'est y = ax + b.
Il te suffit de deux points pour trouver la valeur de a et de b.
Si tu as un premier point (x1;
Y1) et un deuxième point (x2;
{ y1 = ax1 + b.
{ y2 = ax2 + b.
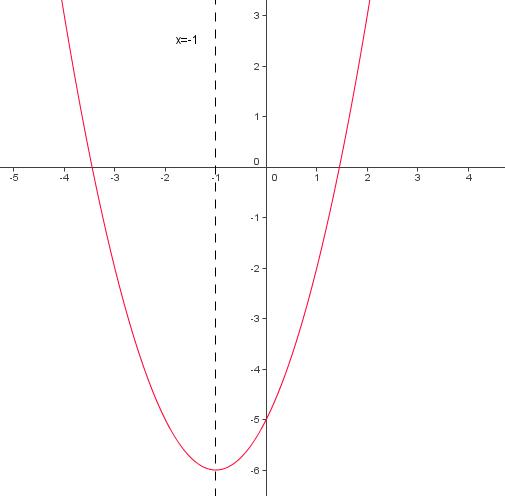
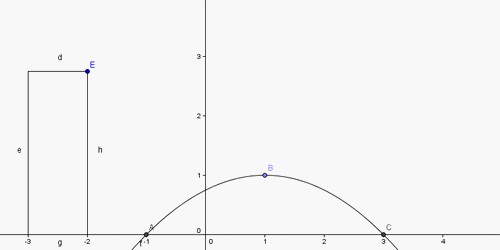
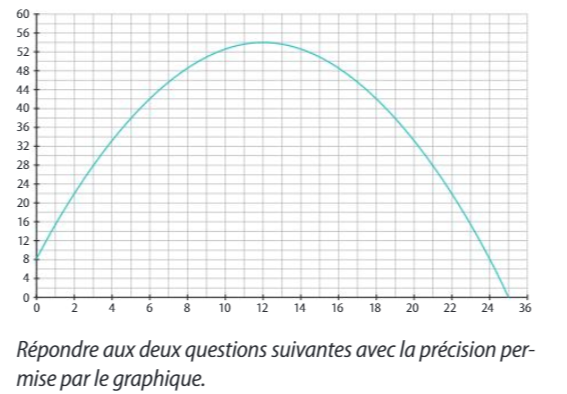
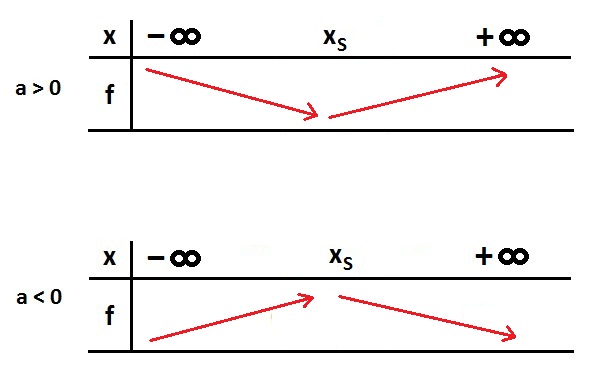
Déterminer, à partir du graphique, quelles sont les coordonnées du sommet de la parabole.
Le sommet est le point le plus bas d'une parabole qui s'ouvre vers le haut.
Déterminer l'équation de la parabole dont le sommet est le point s de coordonné ( 2;
Bienvenue sur la fiche d'exercices de maths la recherche de l'équation à partir d'un graphique (a) de la page dédiée aux fiches d'exercices de maths sur l'algèbre de mathslibres. com.
Vous pouvez l'imprimer, la télécharger, ou.
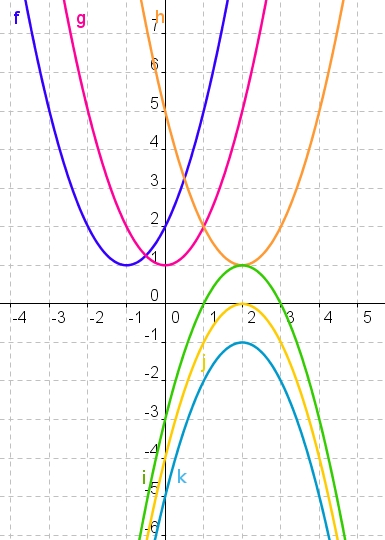
La représentation graphique d'une fonction polynôme du second degré définie sur par (avec a un réel non nul, b et c deux réels) est une parabole.
Cette parabole admet un axe de symétrie vertical d'équation.
Le sommet de la parabole est le point de la parabole d'abscisse.
Les branches de la paraboles sont tournées vers le haut lorsque.
Équation d'une fonction a partir d'un graphique pour complétion, si on veut décrire une courbe (lisse, au sens intuitif et commun du terme!) qui passe par un certain nombre de points (et qui vérifie éventuellement certaines conditions aux.
Fonction racine et exposant fractionnaire.
Trouver le domaine d'une fonction algébrique.
Fonction quadratique (parabole) une fonction quadratique est une fonction polynomiale du second degré dont l'équation est de la forme.
F(x) = ax2 + bx + c.
Où a, b et c ∈ r, (a ≠ 0).
Bonjour, je n'arrive pas à trouver comment calculer l’équation d'une fonction à partir de deux ou trois points (du dessin en fait, mais je n'ai pris que les coordonnées de points ne contenant pas de décimale).
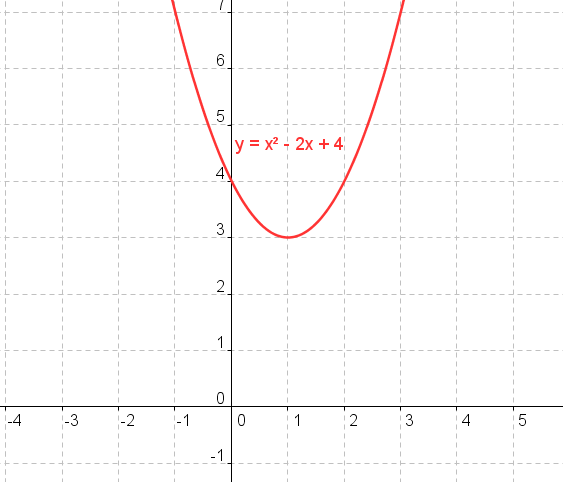
Tracer la parabole d'équation :
Cette équation est sous forme canonique :
Est le couple de coordonnées du sommet de la parabole.
Ici, ce couple est.
Si , la fonction est concave sur , ce qui signifie que la parabole est.
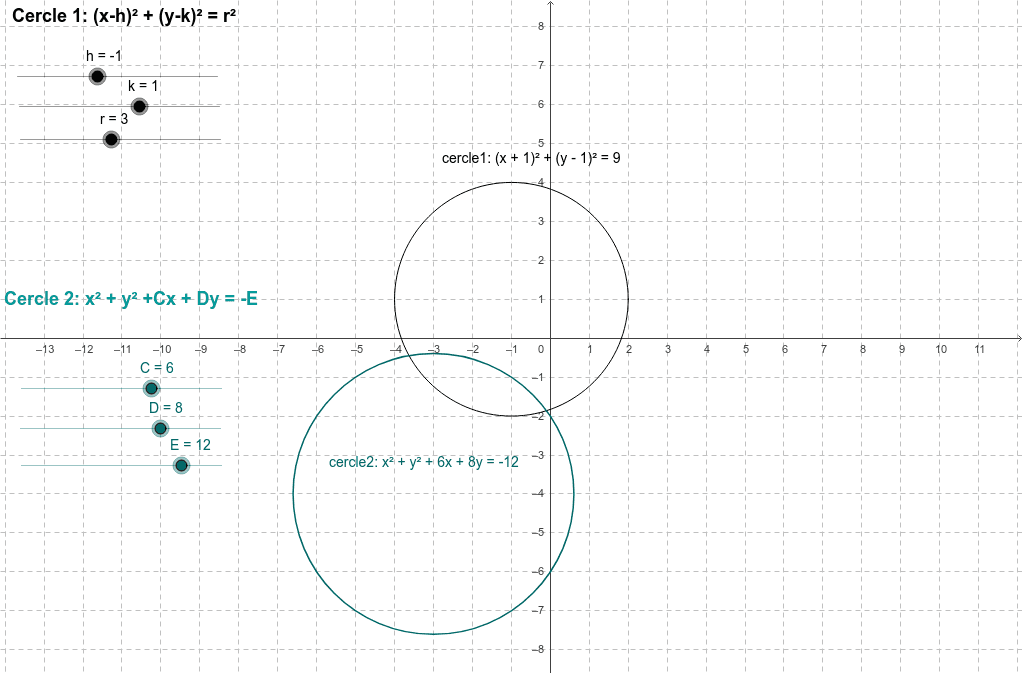
La parabole fait partie des coniques.
Elle s’obtient par l’intersection d’une surface conique et d’un plan.
Une parabole est le lieu géométrique de tous les points situés à égale distance d’une droite fixe, appelée directrice, et d'un point fixe, appelé foyer.
Les propriétés de la parabole.
Cette vidéo explique la méthode algébrique pour déterminer l'équation à partir de:(1) ses coordonnées à l'origine(2) son sommet et un point
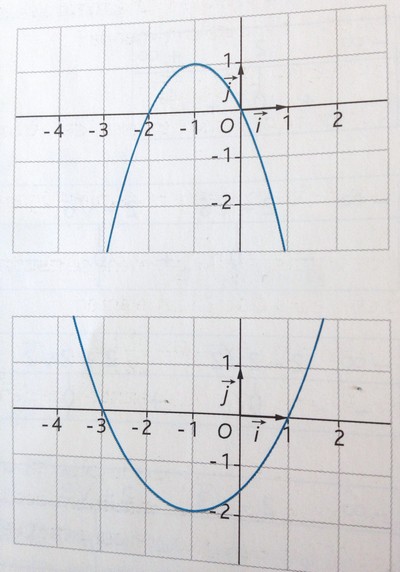
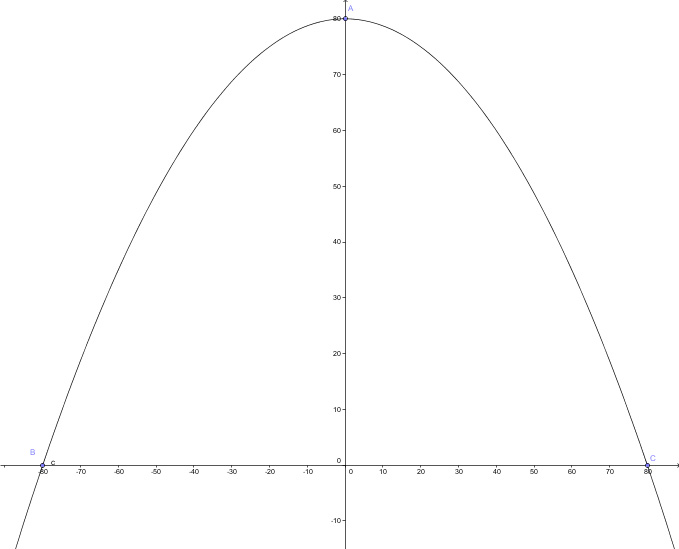
Bonjour, on me demande de trouver l'équation f(x) d'une parabole à partir d'un graphique.
Dans la logique, je sais réaliser cela, mais j'ai un problème au niveau des solutions, le sommet de la parabole se trouve pile sur l'axe des abscisses, permettant ainsi de ne trouver que x1, et pas de x2, donc je ne vois pas comment suivre cette méthode :