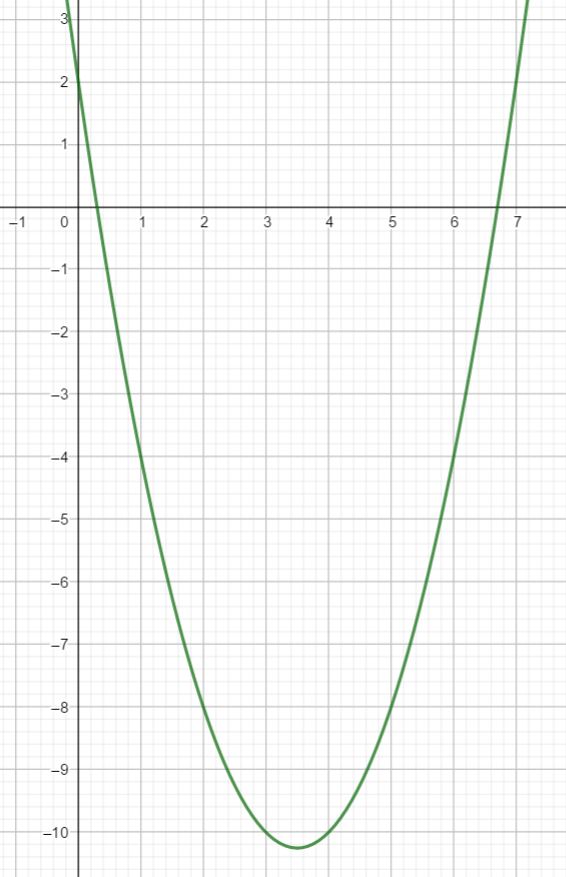
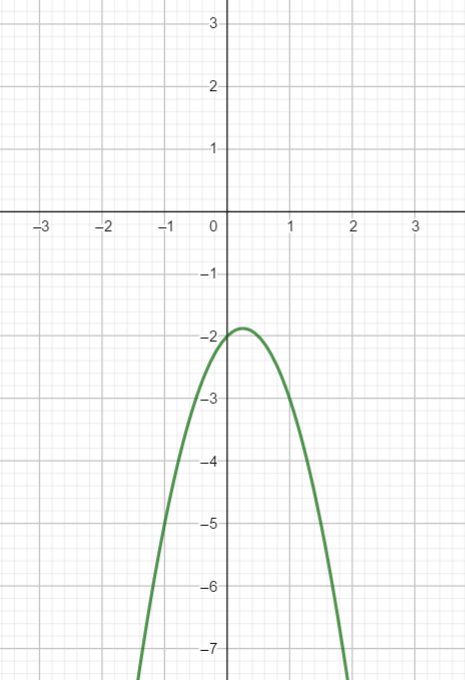
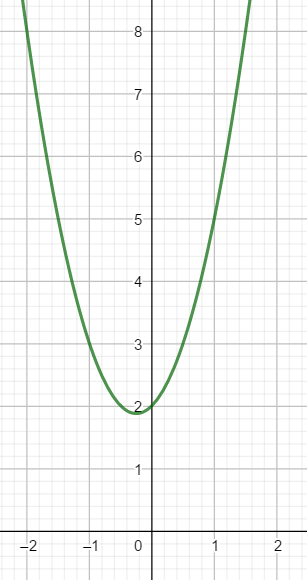
J'ai un exercice avec seulement une courbe, je dois définir la l'expression algébrique de cette fonction mais je ne sais pas comment procédé.
Déterminer l'expression algébrique d une fonction affine à partir de sa représentation graphiquecette vidéo est issue de la bibliothèque instrumenpoche de se.
Je dois trouver grâce aux courbes, l'expression d'une fonction.
Trouver l'expression d'une fonction périodique à partir de sa courbe.
On donne la courbe représentative d'une fonction trigonométrique.
Il faut déterminer si son équation est de la forme y = asin (bx) + c ou de la forme y = acos (bx) + c et retrouver les valeurs de a, b et c.
Créé par sal khan.
Par contre, il faut connaître le type de fonction par lequel tu veux approximer ton nuage de point.
Ceci nécessite d'avoir un modèle de la situation qui a conduit à l'obtention de ce nuage.
En gros je souhaiterai trouver une fonction qui évolue moins vite que la fonction affine, mais plus vite que la fonction logarithme népérien.
L'équation y= (x) est l'équation de la courbe représentative de la fonction.
Cela s'appelle une équation différentielle, dont les plus.
Pardon, le point a a les coordonnes (2;1) :
Retrouver la fonction à partir de la courbe.
À la forme factorisé cela donne:
Là, tu viens de donner un polynome de degré 3 au moins.
Une fois que tu as ton polynome de degré 2 qui colle aux racines, il est valable à un coefficient non nul près.
À partir de ces 3 informations, tu dois trouver 3 équations puis résoudre le système des 3 équations dont les inconnues sont a, b et c.
On rappelle qu'une fonction affine f est représentée par une droite et admet une expression de la forme f\left (x\right)=ax+b.
F est une fonction affine, elle a une expression de la forme f\left (x\right) = ax+b, avec :
A le coefficient directeur de la droite.
B l'ordonnée à l'origine.
Déterminer graphiquement une fonction affine par son coefficient directeur et son ordonnée à l'origine.
Fonction comportant une exponentielle on considère une fonction ƒ définie, sur , par :
Ƒ(x) = (a x2 + bx + c)e−x.
On note c sa représentation graphique dans un repère (o, rr ij,).
On sait que la courbe c passe par le point a(0 ;
1) et qu'elle admet une tangente parallèle à (ox) au point d'abscisse 1.
On sait aussi que ƒ.
Pour tracer la courbe vous avez du calculer des valeurs à l'aide d'une formule.
Cette formule doit nécessairement représenter la fonction que représente la courbe.
Y = a. x donne une droite passant par l'origine des axes.
Y= ax + b droite coupant l'axe y en b.
Y = ax² + bx + c c'est une parabole etc.
Il est possible de représenter par une courbe une fonction définie par une formule ou un tableau de valeurs mais une courbe est également un outil qui permet de définir une fonction.
Elle doit nécessairement respecter l'une des caractérisques des fonctions qui est de n'associer à un nombre de l'ensemble de définition qu'un seul point.